Business valuation is a complex area that underpins a critical part of modern finance. Equity markets, venture capital markets, and debt markets all rely on accurate valuation metrics to help with efficient allocation of capital. Effective valuation tools are also important in business disputes, where lawyers help firms to sort out complex issues related to everything from merger deals to antitrust cases.

Unfortunately, most valuation firms tend to use the simplest and most limited set of tools for valuation – the income approach, sales approach, and replacement cost approach – when valuing a firm. These three methods are effective in simple cases or where firms have stable and predictable profit levels. Yet businesses with stable and predictable profit levels are often the least likely firms to be involved in legal proceedings. Instead, the firms that face legal issues and need to be valued are often those that are the most unorthodox. In these circumstances, the traditional three methods of business appraisers are the least effective. Instead, attorneys and business owners dealing with these situations need to value the company in question based upon real options techniques. These valuation methods are significantly different, but more accurate and effective than traditional methods.

Establishing these real options-based valuations requires determining what methods are most appropriate in a given set of circumstances. Larger and better established firms rely on valuations that focus on their current cash flows extrapolated into the future at some rate of growth. These cash flows form the basis for what investors will pay for a stock for instance. On the other hand, smaller firms and faster growing firms need to be valued differently. Firms that fit this mold often have negligible cash flows upfront compared to the cash flows that they will generate in the future – if all goes according to plan with the firm. That latter complication – the significant risks associated with projected future cash flows create both opportunities and uncertainties in the future. That necessitates alternative valuation metrics.

The crux of modern asset valuation is based on a concept called the time value of money. Essentially the idea is that because money received in the future is worth less than money received today, we can value assets or a business based on their associated cash flows and an appropriate discount rate. This approach forms the basis of everything from stock valuation on Wall Street to proper methods for computing interest rates in bankruptcy. This facet of valuation is well understood. But what about the future opportunities or chances of cash flows that are uncertain?  That’s what embedded options address.

The concept of embedded options might seem abstract or even too nebulous for many judges to buy into in a court case, but the reality is that real options have significant value and are often a subject of serious financial negotiations. Particularly for small firms, real options are often important and serve as the basis for various types of convertible debt and warrant grants. Essentially, real options increase in value in situations where there is greater uncertainty, and when interest rates in the broader economy rise.

These volatile situations are often the very situations that lead to court cases for attorneys – a business deal that went wrong leads to a bankruptcy but could have led to a hugely successful company, a merger agreement could result in substantial cost savings for both firms or substantial value destruction for investors and is being challenged by shareholders, a wrongful death case for an individual in the prime of their lives leaves so many possible futures unexplored. Thanks to new statistical techniques and greater computing power, these situations and others can be effectively modeled through computer simulations and valued by economists in ways that would have been unimaginable a decade ago.

In this article, we will explore three different methods for valuing firms and assets based on real options. These methods are extremely important when considering the valuation of start-up firms, fast growing companies, firms that are currently losing money, and firms that have large amounts of potentially valuable intangible property like patents.

Black Scholes Model

The Black-Scholes model for calculating the premium of an option was introduced in 1973 in a paper entitled, "The Pricing of Options and Corporate Liabilities" published in the Journal of Political Economy. The formula, developed by three economists – Fischer Black, Myron Scholes and Robert Merton – is perhaps the world's most well-known options pricing model. Black passed away two years before Scholes and Merton were awarded the 1997 Nobel Prize in Economics for their work in finding a new method to determine the value of derivatives.

The Black-Scholes model is used to calculate the theoretical price of European put and call options, ignoring any dividends paid during the option's lifetime. The model is used chiefly with publicly traded options, but as will be seen later, the concept can be extended to use in private company situations including those involving start-ups and patents.

While the original Black-Scholes model did not take into consideration the effects of dividends paid during the life of the option, the model can be adapted to account for dividends by determining the ex-dividend date value of the underlying stock.

The model makes certain assumptions, including:

1. The options are European and can only be exercised at expiration

2.  No dividends are paid out during the life of the option

3.   Efficient markets (i.e., market movements cannot be predicted)

4.  No commissions

5. The risk-free rate and volatility of the underlying are known and constant

6.  Follows a lognormal distribution; that is, returns on the underlying are normally distributed.

The formula, shown in Figure 4, takes the following variables into consideration:

1.  Current underlying price

2. Options strike price

3.  Time until expiration, expressed as a percent of a year

4.  Implied volatility

    Risk-free interest rates

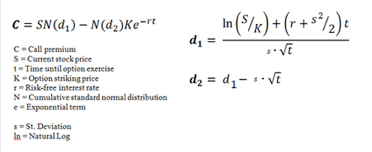
The model is essentially divided into two parts: the first part, SN(d1), multiplies the price by the change in the call premium in relation to a change in the underlying price. This part of the formula shows the expected benefit of purchasing the underlying outright. The second part, N(d2)Ke^(-rt), provides the current value of paying the exercise price upon expiration (remember, the Black-Scholes model applies to European options that are exercisable only on expiration day). The value of the option is calculated by taking the difference between the two parts, as shown in the equation above.

The Black-Scholes method is most often appropriate for business valuation when businesses:

1. Are growing sales very rapidly

2. Are in a market or industry where the distribution of firm profits is likely to be normally distributed (i.e. a few firms will be enormously profitable and a few will be very unprofitable, but most will be somewhere in between)

3. Possess patents or other intangible property which has clear value, but does not lend itself well to traditional asset appraisal methodologies

Under these circumstances, the Black Scholes method can provide a valuation that is dramatically different from and more accurate than traditional income based ratio methods.

Binomial Options Pricing Model

The Cox-Rubenstein (or Cox-Ross-Rubenstein) binomial option pricing model is a variation of the original Black-Scholes option pricing model. It was first proposed in 1979 by financial economists/engineers John Carrington Cox, Stephen Ross and Mark Edward Rubenstein. The model is popular because it considers the underlying instrument over a period of time, instead of just at one point in time, by using a lattice based model.

A lattice model takes into account expected changes in various parameters over an option's life, thereby producing a more accurate estimate of option prices than created by models that consider only one point in time. Because of this, the Cox-Ross-Rubenstein model is especially useful for analyzing American style options, which can be exercised at any time up to expiration (European style options can only be exercised upon expiration).

The Cox-Ross-Rubenstein model uses a risk-neutral valuation method. Its underlying principal purports that when determining option prices, it can be assumed that the world is risk neutral and that all individuals (and investors) are indifferent to risk. In a risk neutral environment, expected returns are equal to the risk-free rate of interest.

The Cox-Ross-Rubenstein model makes certain assumptions, including:

1. No possibility of arbitrage; a perfectly efficient market

2. At each time node, the underlying price can only take an up or a down move and never both simultaneously

The Cox-Ross-Rubenstein model employs and iterative structure that allows for the specification of nodes (points in time) between the current date and the option's expiration date. The model is able to provide a mathematical valuation of the option at each specified time, thereby creating a "binomial tree" - a graphical representation of possible values at different nodes.

The Cox-Ross-Rubenstein model is a two-state (or two-step) model in that it assumes the underlying price can only either increase (up) or decrease (down) with time until expiration. Valuation begins at each of the final nodes (at expiration) and iterations are performed backwards through the binomial tree up to the first node (date of valuation). In very basic terms, the model involves three steps:

1.) The creation of the binomial price tree

2.) Option value calculated at each final node

3.) Option value calculated at each preceding node

The binomial pricing method is most useful in situations where industries are likely to be distorted due to natural monopolies and significant economies of scale. In these situations, the distribution of eventual profits is not normally distributed. As a result, the Black-Scholes method is poorly suited to the situation, while the binomial method is more useful. However, the binomial valuation method does assume efficient markets which in the context of business valuation requires that there be multiple potential buyers for a business who would all get similar value from the firm’s assets.

Monte Carlo Simulation

Both the Black-Scholes approach and the Binomial approach can make sense for many unique business valuation needs, but each requires specific assumptions and circumstances. The most flexible method of business valuation is uses Monte Carlo simulation. However, Monte Carlo simulation also requires the most time and effort to effectively carry out.

Essentially a Monte Carlo simulation is simply a series of statistical exercises each of which results in a different value for the business. Each statistical exercise represents in essence a possible business valuation under different circumstances and if different events occur in the future.

Since there is no way to predict the future, the Monte Carlo simulation runs hundreds of times allowing one to determine the percentage chance that a business will achieve different levels of valuation. For instance, a Monte Carlo simulation might report that 5% of the time a business is worth more than $1 million, 10% of the time it is worth between $950,000 and $1 million, 15% of the time the business is worth between $900,000 and $950,000, etc.

Using this distribution of probabilities and values, one can determine an “expected” business valuation which in essence represents an average across all of the different scenarios explored by the Monte Carlo simulation. Monte Carlo simulations are routinely used to value complex financial securities and typically thousands of exercises are run in the simulation. As a result, Monte Carlo simulations are a well-accepted and well-regarded tool in finance. Unfortunately, its complexity has limited the spread of the tool beyond the echelons of higher finance.

Monte Carlo simulations are best suited to situations where:

1. A wide range of possible outcomes for a  firm could occur in the future

2. Firm value is sufficiently high to warrant the work of setting up a Monte Carlo simulation

3. The firm’s range of future prospects can be effectively modeled mathematically by an experienced analyst

Conclusion

Overall, the field of business valuation is held back by its reliance on the three traditional valuation metrics despite the fact that these methods are often limited and ineffective for businesses that are (1) growing quickly, or (2) financially troubled, or (3) in an industry with limited competition, or (4) have experienced a significant change in the nature of the business recently.

In these circumstances, three alternative valuation methods are more appropriate. These are the Black-Scholes method, the Binomial Options Pricing method, and the Monte Carlo Simulation method. Each of these methods is appropriate in different circumstances, but between the three they provide an effective toolset for evaluating firm valuation in almost any circumstances.

Attorneys, financial advisors, and business owners dealing with circumstances involving valuation are abrogating an important element of their obligations if they do not consider whether one of these alternative valuation methods is more appropriate in all business cases. At a minimum, consideration of these methods gives the firm a robust set of options to consider. Without such consideration, a firm is implicitly assumed to fit into a very narrowly defined set of parameters. That assumption is a disservice to stakeholders.